Треугольный массив
При изгибании отрезка мы изменяем лишь z-координату его середины, поэтому теоретически можно использовать пару координат [x, y] как индекс в таблице со значениями z. Однако такой массив получится весьма разреженным, а с нормальным, непрерывным массивом программа работает намного быстрее — ей не приходится тратить время на просмотр списков разреженного массива. Именно по этой причине в листинге 8.1 определена система двумерных логических адресов (тип данных TVertex), в которые «отображаются» фактические трехмерные координаты (тип данных Ttriple).
Листинг 8.1. Модуль GLOBAL.PAS
unit Global; {Fractal Landscapes 3.0 - Copyright © 1987..1996, Джон Шемитц} interface uses WinTypes; type Int16 = {$ifdef Ver80} integer {$else} SmallInt {$endif} ; const MaxPlys = 8; MaxEdgeLength = 1 shl (MaxPlys - 1); UnitLength: LongInt = 5000; ShadesOfGray = 64; type TCoordinate = -30000..30000; TTriple = record X, { Ширина: от 0 (слева) до UnitLength (справа)} Y, { Глубина: от 0 (спереди) до VanishingPoint.Y (сзади)} Z: TCoordinate; { Высота: от 0 (снизу) до UnitLength (сверху)} end; function Triple(X, Y, Z: TCoordinate): TTriple; type TPixel = TPoint; type GridCoordinate = 0..MaxEdgeLength; { Треугольная сетка } TVertex = record AB, BC, CA: GridCoordinate; end; function Vertex(AB, BC, CA: GridCoordinate): TVertex; type DrawModes = (dmOutline, dmFill, dmRender); DrawRates = (drLow, drMedium, drHigh); const Envelope = 3000; SeaLevel: word = 100; { от 0 (снизу) до UnitLength (сверху)} VanishingPoint: TTriple = ( X: 1500 ; Y: 25000 ; { Видимая глубина точки перспективы } Z: 15000 ); LightSource: TTriple = ( X: 2500; Y: +7500; Z: 25000 ); DrawMode: DrawModes = dmOutline; DrawRate: DrawRates = drHigh; const Uninitialized = -30000; var A, B, C: TVertex; Plys: 1..MaxPlys; EdgeLength: Int16; DisplayHeight, DisplayWidth: Int16; implementation function Triple(X, Y, Z: TCoordinate): TTriple; begin Result.X := X; Result.Y := Y; Result.Z := Z; end; function Vertex(AB, BC, CA: GridCoordinate): TVertex; begin Result.AB := AB; Result.BC := BC; Result.CA := CA; end; end.Вероятно, простейшая схема такого отображения заключается в нумерации всех вершин вдоль каждой из трех сторон внешнего треугольника (см. левую половину рис. 8.6) и использовании всех трех координат для вершин каждой стороны. Хотя в действительности нам нужны лишь две координаты, а третья избыточна, я предпочитаю ссылаться на внешние вершины треугольника в чуть более понятном виде [1, 0, 0], [0, 1, 0] и [0, 0, 1] вместо [1, 0], [0, 1] и [0, 0]. Именно по этой причине тип TVertex определяется в виде тройки координат, несмотря на то что третья координата в принципе не нужна и даже слегка замедляет вычисления.
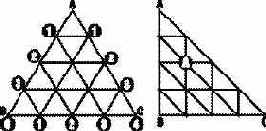
Рис. 8.6. Сохранение вершин в «квадратном» массиве
Впрочем, когда дело доходит до базы данных вершин, третья координата действительно игнорируется. Как видно из правой половины рис. 8.6, координаты вершин сохранятся и в том случае, если равносторонний треугольник преобразовать в прямоугольный. Поэтому координаты AB и BC можно будет использовать так, словно они относятся к элементу «квадратного» массива.
Однако сохранение нашего «треугольного» массива в «квадратном» означало бы, что почти половина места в массиве пропадает даром. В принципе в этом нет ничего страшного, хотя в 16-разрядной среде мы бы столкнулись с ограничением на размер сегмента (64 Кб). Каждый элемент типа TTriple состоит из трех 16-разрядных чисел с фиксированной точкой, поэтому квадратный массив после восьми итераций деления сторон (рис. 8.7) будет содержать (28-1 + 1)2 вершин, или 99 846 байтов. Если же сохранять только вершины, принадлежащие диагонали или находящиеся под ней, объем сокращается до 50 310 байтов. В этом случае можно воспользоваться простым индексированием вместо huge-указателей и массивов. К тому же вся база данных (по крайней мере в данной демонстрационной программе) помещается в одном сегменте данных, что ускоряет доступ к ней по сравнению с дополнительным выделением блоков из пула и использованием указателей.
Поскольку восемь итераций вряд ли можно назвать слишком мелким делением для экрана 1280?1024, описанная в этой главе программа Fractal Landscapes 3.0 (она же FL3 — переработанная (сначала под Windows, а затем для Delphi) версия DOS-программы, изначально написанной «для души» на Turbo Pascal 4.0) использует «треугольную» структуру базы данных (см. листинг 8.2). Основная идея заключается в том, что каждый ряд вершин хранится в базе после предыдущего ряда. Поскольку первый ряд состоит всего из одной вершины, второй ряд начинается со второй «ячейки». Он состоит из двух вершин, поэтому третий ряд начинается с четвертой ячейки, и так далее.
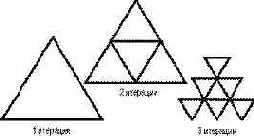
Рис. 8.7. Процесс многократного деления
Листинг 8.2. Модуль DATABASE.PAS
unit Database; { Fractal Landscapes 3.0 - Copyright © 1987..1997, Джон Шемитц } { База данных и генерация ландшафта } interface uses SysUtils, Global; { Вспомогательные математические функции } function IDIV(Numerator: LongInt; Denominator: Int16): Int16; {$ifdef Ver80} {В Delphi 1.0 еще поддерживаются InLine-функции} InLine( $5B / { POP BX ; Делитель } $58 / { POP AX ; Младшее слово делимого } $5A / { POP DX ; Старшее слово делимого } $F7 / $FB { IDIV BX ; Частное } {$endif} function IMUL(A, B: Int16): LongInt; {$ifdef Ver80} {В Delphi 1.0 еще поддерживаются InLine-функции} InLine( $5B / { POP BX } $58 / { POP AX } $F7 / $EB { IMUL BX } ); {$endif} function Rand(Envelope: integer): integer; { База данных } procedure ResetDB; function GetTriple(const V: TVertex): TTriple; { DB[V] } procedure SwapTriples(var A, B: TTriple); function Midpoint(A, B: TVertex): TVertex; function LoadLandscape(const FileName: TFileName) : boolean; function SaveLandscape(const FileName: TFileName) : boolean; { Вычисления } procedure FractureTriangle(const A, B, C: TVertex; Plys: word); function Unscale(ScaledCoordinate: LongInt): TCoordinate; {$ifdef Ver80} {В Delphi 1.0 еще поддерживаются InLine-функции} InLine( $58 / { POP AX ; младшее слово SC } $5A / { POP DX ; старшее слово SC } $8B / $1E / UnitLength / { MOV BX,[UnitLength] ; младшее слово масштабного коэффициента} $F7 / $FB { IDIV BX ; Обратное масштабирование } ); {$endif} implementation { Вспомогательные математические функции } {$ifNdef Ver80} { В 32-разрядных версиях Delphi InLine-функции не поддерживаются } function IDIV(Numerator: LongInt; Denominator: Int16): Int16; begin Result := Numerator div Denominator; end; {$endif} {$ifNdef Ver80} { В 32-разрядных версиях Delphi InLine-функции не поддерживаются } function IMUL(A, B: Int16): LongInt; begin Result := Longint(A) * B; end; {$endif} function Rand(Envelope: integer): integer; { Псевдонормальное распределение в интервале ±Envelope } begin Rand := integer(Random(Envelope)) + integer(Random(Envelope)) - Envelope; end; {$ifNdef Ver80} {В 32-разрядных версиях Delphi InLine-функции не поддерживаются } function Unscale(ScaledCoordinate: LongInt): TCoordinate; begin Result := ScaledCoordinate div UnitLength; end; {$endif} { База данных } var DB: array[0..8384] of TTriple; { Треугольный массив: (MEL+1) элементов } NumberOfVertices, TopRow: word; Envelopes: array[1..MaxPlys] of word; function Vertices(N: word): word; { Число вершин, содержащихся в равностороннем треугольнике с длиной стороны N-1 } begin Vertices := (Sqr(N) + N) shr 1; end; function Midpoint(A, B: TVertex): TVertex; begin Result := Vertex( (A.AB + B.AB) shr 1, { среднее } (A.BC + B.BC) shr 1, (A.CA + B.CA) shr 1 ); end; function Loc(const V: TVertex): word; begin Loc := NumberOfVertices - Vertices(TopRow - V.AB) + V.BC; { ^^^^^^^^^^^^^^^^^^ На самом деле это не нужно и приводит к напрасным затратам времени, но сохранено для совместимости с .FL-файлами программы FL2. } end; procedure SetTriple(var V: TVertex; var T: TTriple); { DB[V] := T } begin DB[Loc(V)] := T; end; function GetTriple(const V: TVertex): TTriple; { DB[V] } begin Result := DB[Loc(V)]; end; procedure SwapTriples(var A, B: TTriple); var Tmp: TTriple; begin Tmp := A; A := B; B := Tmp; end; procedure SwapZ(var A, B: TTriple); var C: TCoordinate; begin C := A.Z; A.Z := B.Z; B.Z := C; end; const Uninitialized = -30000; procedure ResetDB; var T: TTriple; R, Theta: double; I, Offset: integer; tA, tB, tC: TTriple; const Base_Rotation = - Pi / 2.1; { Поворот против часовой стрелки } RotateBy = Pi * 2 / 3; {120°} begin { Установить параметры, зависящие от числа итераций (Plys) } EdgeLength := 1 shl (Plys - 1); TopRow := EdgeLength + 1; { "Ограничитель" } NumberOfVertices := Vertices(TopRow); for I := Plys downto 1 do Envelopes[I] := Envelope shr Succ(Plys - I); { Сбрасываем в исходное состояние NumberOfVertices вершин в базе данных } T.X := Uninitialized; T.Y := Uninitialized; T.Z := Uninitialized; for I := Low(DB) to High(DB) do DB[I] := T; { Теперь задаем положение "определяющих" (то есть внешних) точек A, B и C } A.AB := 0; A.BC := EdgeLength; \A.CA := 0; B.AB := 0; B.BC := 0; B.CA := EdgeLength; C.AB := EdgeLength; C.BC := 0; C.CA := 0; { Рассчитываем для них тройки координат } Offset := UnitLength div 2; R := UnitLength / 2; Theta := Base_Rotation; tA := Triple( Round(R * Cos(Theta)) + Offset, Round(R * Sin(Theta)) + Offset, SeaLevel + Rand(Envelope) ); Theta := Theta + RotateBy; tB := Triple( Round(R * Cos(Theta)) + Offset, Round(R * Sin(Theta)) + Offset, SeaLevel + Rand(Envelope) ); Theta := Theta + RotateBy; tC := Triple( Round(R * Cos(Theta)) + Offset, Round(R * Sin(Theta)) + Offset, SeaLevel + Rand(Envelope) ); { По крайней мере одна точка должна находиться над уровнем моря } if (tA.Z < SeaLevel) AND (tB.Z < SeaLevel) AND (tC.Z < SeaLevel) then repeat tB.Z := SeaLevel + Rand(Envelope); until tB.Z > SeaLevel; { Сделаем A самой нижней точкой... } if tA.Z > tB.Z then SwapZ(tA, tB); if tA.Z > tC.Z then SwapZ(tA, tC); SetTriple(A, tA); SetTriple(B, tB); SetTriple(C, tC); end; function SaveLandscape(const FileName: TFileName): boolean; var Handle: integer; begin try Handle := FileCreate(FileName); try Result := (FileWrite(Handle, Plys, SizeOf(Plys)) = SizeOf(Plys)) and (FileWrite(Handle, DB, NumberOfVertices * SizeOf(TTriple)) = NumberOfVertices * SizeOf(TTriple)); finally FileClose(Handle); end; except on Exception {любое исключение} do Result := False; end; end; function LoadLandscape(const FileName: TFileName): boolean; var Handle: integer; begin Result := False; try Handle := SysUtils.FileOpen(FileName, fmOpenRead); try if FileRead(Handle, Plys, SizeOf(Plys)) = SizeOf(Plys) then begin ResetDB; LoadLandscape := FileRead( Handle, DB, NumberOfVertices * SizeOf(TTriple)) = NumberOfVertices * SizeOf(TTriple); end; finally FileClose(Handle); end; except on Exception {любое исключение} do Result := False; end; end; { Основные действия } procedure FractureLine( var vM: TVertex; const vA, vB: TVertex; Envelope: integer ); var A, B, M: TTriple; begin vM := Midpoint(vA, vB); M := GetTriple(vM); if M.X = Uninitialized then { Еще не задано } begin A := GetTriple(vA); B := GetTriple(vB); M := Triple( A.X + (B.X - A.X) div 2, A.Y + (B.Y - A.Y) div 2, A.Z + (B.Z - A.Z) div 2 + Rand(Envelope) ); { Средняя высота ± Random(Envelope) } SetTriple(vM, M); end; end; procedure FractureTriangle(const A, B, C: TVertex; Plys: word); var Envelope: word; AB, BC, CA: TVertex; begin if Plys > 1 then begin Envelope := Envelopes[Plys]; FractureLine(AB, A, B, Envelope); FractureLine(BC, B, C, Envelope); FractureLine(CA, C, A, Envelope); Dec(Plys); FractureTriangle(CA, BC, C, Plys); FractureTriangle(AB, B, BC, Plys); FractureTriangle(BC, CA, AB, Plys); FractureTriangle(A, AB, CA, Plys); end; end; end.